INTRODUCTION
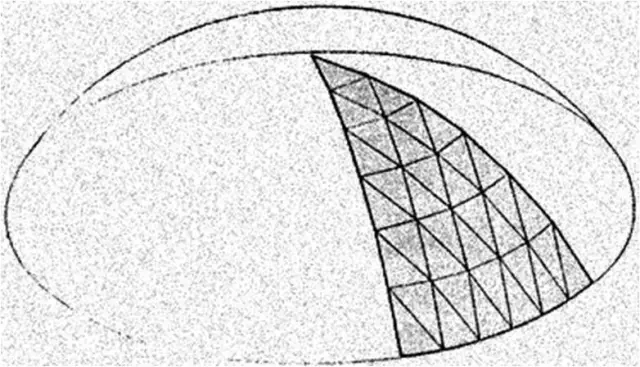
A geodesic dome is more than a collection of triangles. The underlying geometric symmetry, strength and spaciousness of the dome combine to create a feeling of wholeness that is not predicted by simple addition of the individual triangles.

- Geodesic domes require no load bearing interior walls to support the roof.
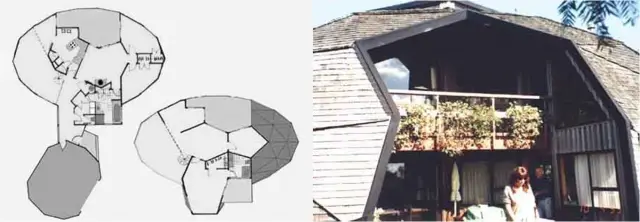
- Interior variations for floor plans within the dome are almost limitless.
- Interior partitions can be framed directly into the dome shell or may be free standing non structural space divisions.
- Sound and visual privacy, floor plan efficiency and human scale can all be maintained.
- Unique interior advantages of the dome include: greater freedom of floor plan design;
- Cathedral ceilings without custom design; and unparalleled evenness of light, heat and sound distribution.
In addition to the dome’s vast interior variations, the dome shell also offers many exciting exterior possibilities.
- Because of the unique distribution stresses in the dome shell, up to 50% of the lowest ring of triangles can be removed
- These non-load bearing openings can then be replaced by walls with conventional doors and windows or by extensions such as greenhouses, garages, carports, sun porches or other conventional structures.
- Greater integration of the dome to many natural environments without custom design, greater structural strength and minimum violation of ground and air space.
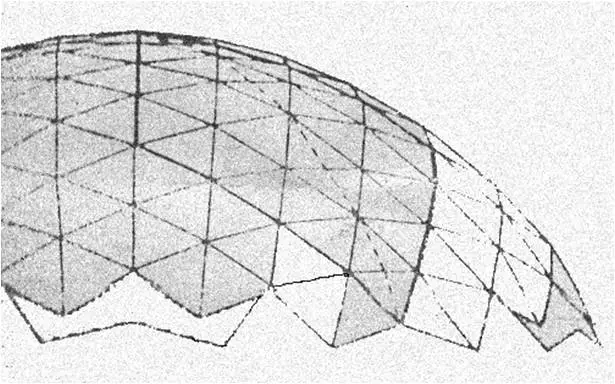

How to construct?
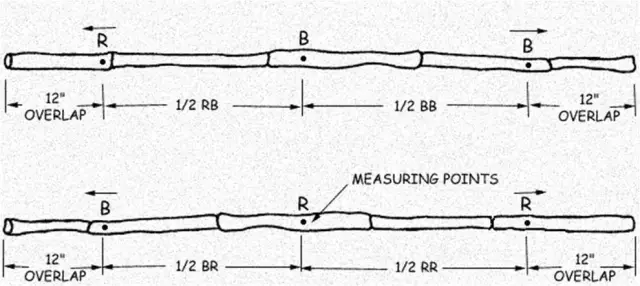
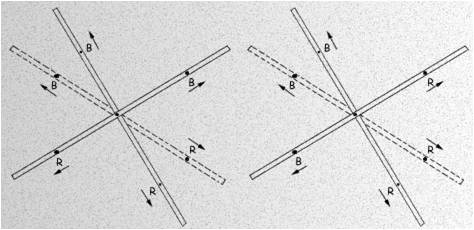
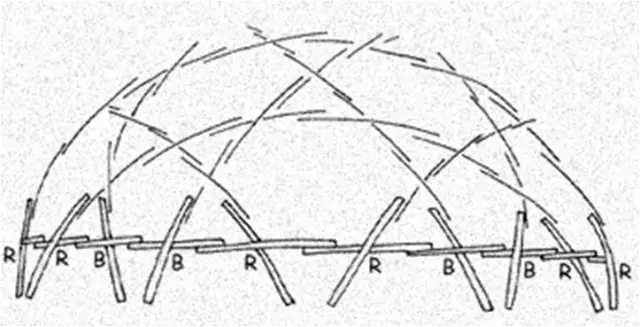
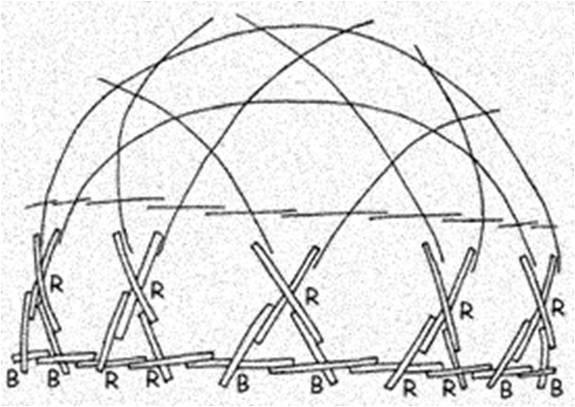
The low cost geodesic dome made of bamboo, as shown in the assembly diagrams, contains two different joints: a B joint which occurs at the vertices of all pentagons formed, and an R joint which occurs at all other points. The spans from joint to joint are BB, BR, or RR.
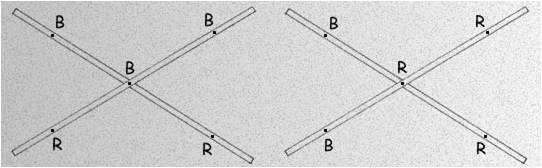
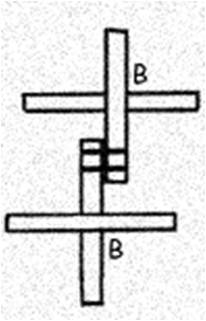
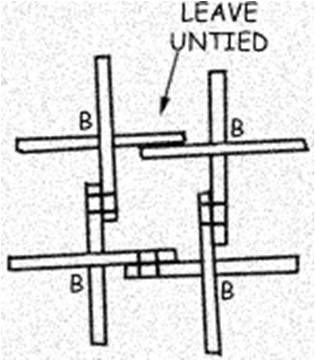
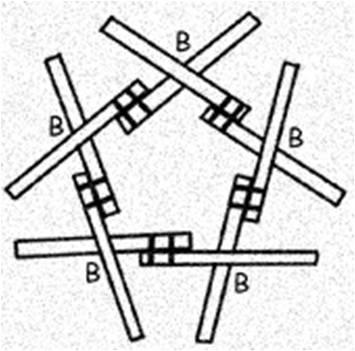
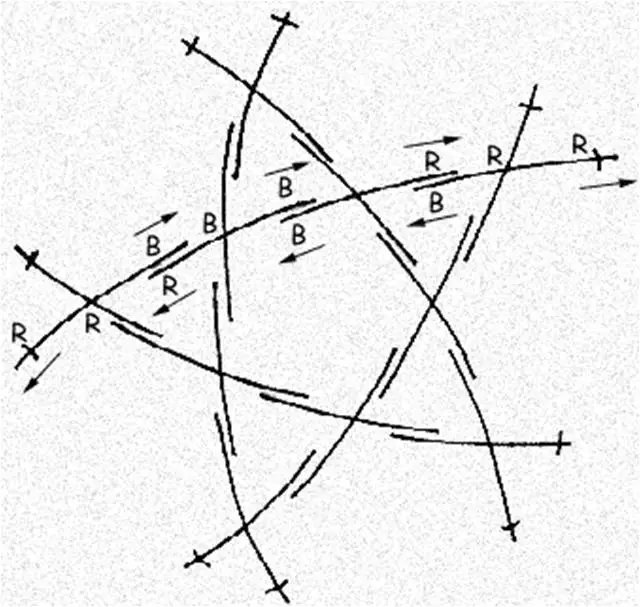
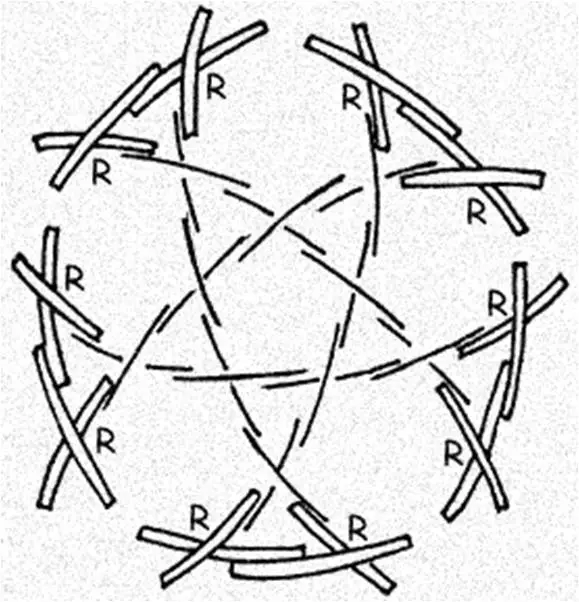
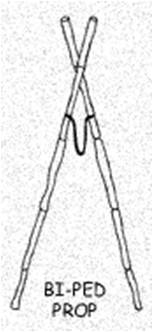
Lift the assembled figure off the ground to facilitate the addition of new crosses. Use five bi-ped props. Each prop consists of two bamboo sticks about 7 feet long, tied together near the top with a cord about a foot long. These props will then support the dome at equidistant points from it’s apex; first at the five vertices at the top of the pentagon, later at five corresponding points on the top five hexagons.
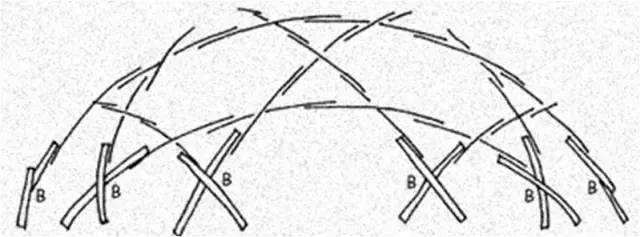


I recommend including the
I recommend including the length ratios between points here. I have found that the tiniest variations in lengths create deformities that are really obvious when you step back and look at the whole ball. B-B = .26r; B-R = .31r; R-R = .326r;